Statistische bewerking van reeksberekeningsresultaten

Methode van de steekproefkwantielen

Sorteer de lijst van overstortingsgebeurtenissen op afnemende grootte van de totale overstortingshoeveelheid per gebeurtenis. Volgens de methode van de steekproefkwantielen kunt u vervolgens aan de x^e-gebeurtenis uit een reeks van gebeurtenissen over één jaar een herhalingstijd definitie Herhalingstijd T (kans van optreden) koppelen volgens:

Neerslagreeks 10 jaar

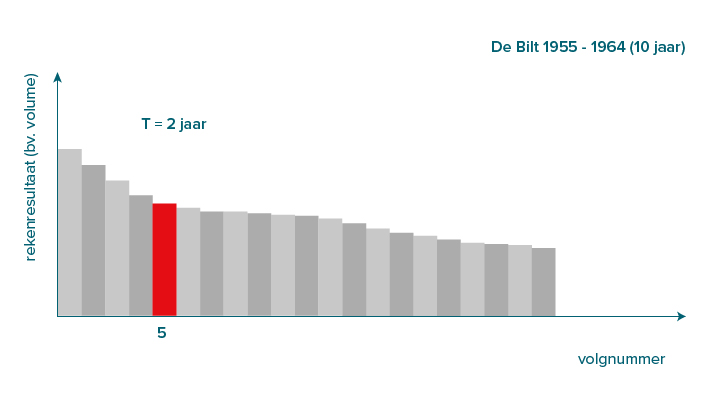
Zo heeft de vijfde gebeurtenis (volgnummer) uit de neerslagreeksresultaten met een lengte van tien jaar een herhalingstijd van één keer per twee jaar (5 jaar/10^e gebeurtenis).

Neerslagreeks 25 jaar

Als u een neerslagreeks met een lengte van 25 jaar gebruikt, heeft de 25e gebeurtenis een herhalingstijd van één keer per jaar. Het volume voor een herhalingstijd van T= 2 jaar berekent u bij een reeks van 25 jaar als het gemiddelde van de twaalfde en dertiende gebeurtenis, ofwel:

In tabel A staan de resultaten van de simulatie van een neerslagreeks van 25 jaar, gesorteerd op volume per gebeurtenis.

In tabel A zijn de overstortingshoeveelheden voor de verschillende herhalingstijden met de methode van de steekproefkwantielen bepaald. Interpreteer de bepaalde volumen met de herhalingstijden T= 10 en 25 jaar voorzichtig, want deze zijn minder betrouwbaar.

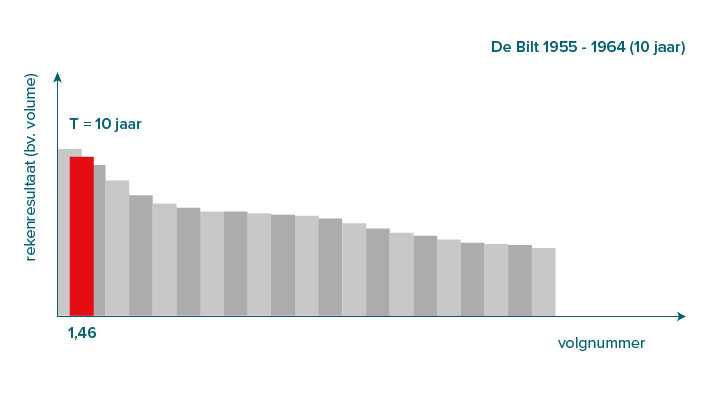
Correctie voor grote herhalingstijden bij reeks van tien jaar

Als vuistregel kunt u aanhouden dat u de herhalingstijd tot T= √n jaar met voldoende betrouwbaarheid kunt bepalen (waarbij n gelijk is aan het aantal jaren in de reeks). De betrouwbaarheid van het bepalen van de overstortingshoeveelheid met een herhalingstijd van één keer per vijf of tien jaar is dus beperkt op basis van de resultaten van een neerslagreeks van tien jaar. In de praktijk is daarom ook wel sprake van de ‘één-keer-per-tien-jaargebeurtenis’ voor de betreffende reeks van tien jaar. Om de onbetrouwbaarheid bij een reeks van tien jaar te ondervangen, is gezocht naar een correctie voor T= 5 en T=10 jaar. Zodat deze beter corresponderen met de resultaten uit de bewerking volgens de methode van de steekproefkwantielen voor T= 5 en T=10 jaar bij een reeks van 25 jaar.

Als u de overstortingshoeveelheden van een reeks van tien jaar sorteert naar afnemende grootte, geeft de volgende correctie een betere benadering:


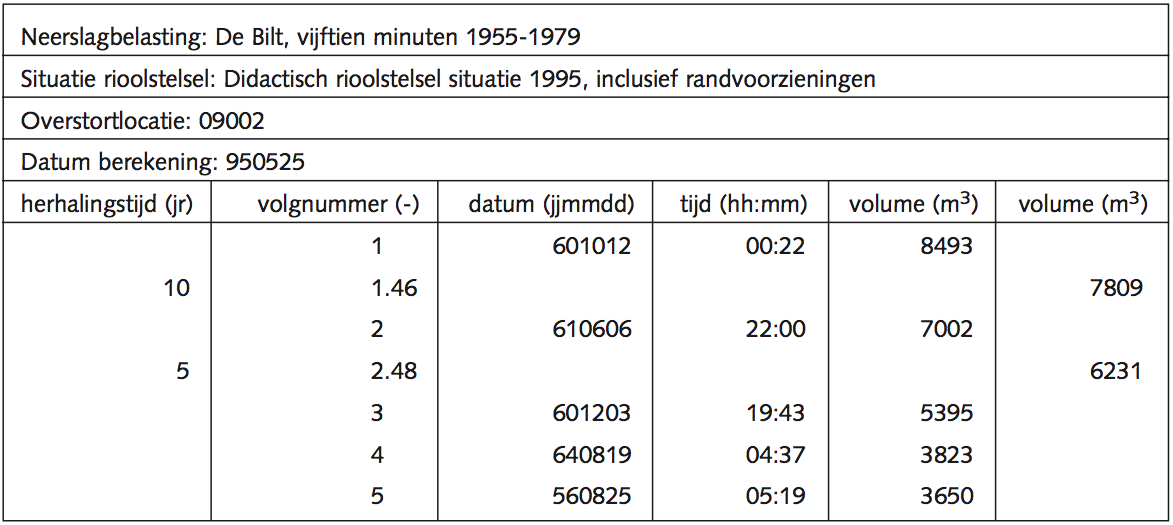
De ‘1,46e gebeurtenis’ heeft dus een herhalingstijd van één keer per tien jaar en de ‘2,48e gebeurtenis’ een herhalingstijd van één keer per vijf jaar. Voor dezelfde overstort definitie Overstort en situatie als in tabel A staan in tabel B de resultaten van de neerslagreeks van tien jaar. Hierbij is de eerder omschreven correctie voor T= 5 en T=10 jaar gebruikt.