Schematisering
Een overstort (intern of extern) schematiseert u als twee knopen met een (korte) overlaat als tussenliggende verbinding. (De zogenoemde lange overlaat komt in de riolering niet of nauwelijks voor en wordt niet behandeld in de Kennisbank.) Maak onderscheid tussen volkomen en onvolkomen overlaten. Bij een volkomen overlaat heeft de benedenstroomse waterstand h2 geen invloed op de stroming over de overlaat, maar wordt deze alleen bepaald door de bovenstroomse waterstand h1. Bij een onvolkomen overlaat heeft de benedenstroomse waterstand juist wel invloed. Bij een benedenstroomse waterstand h2 > 2/3 · h1 is sprake van een onvolkomen overlaat. In een berekening kan de stromingstoestand van een overlaat van volkomen stromingstoestand onvolkomen worden en vice versa. Ook kan bij een onvolkomen overlaat de stroomrichting omdraaien.
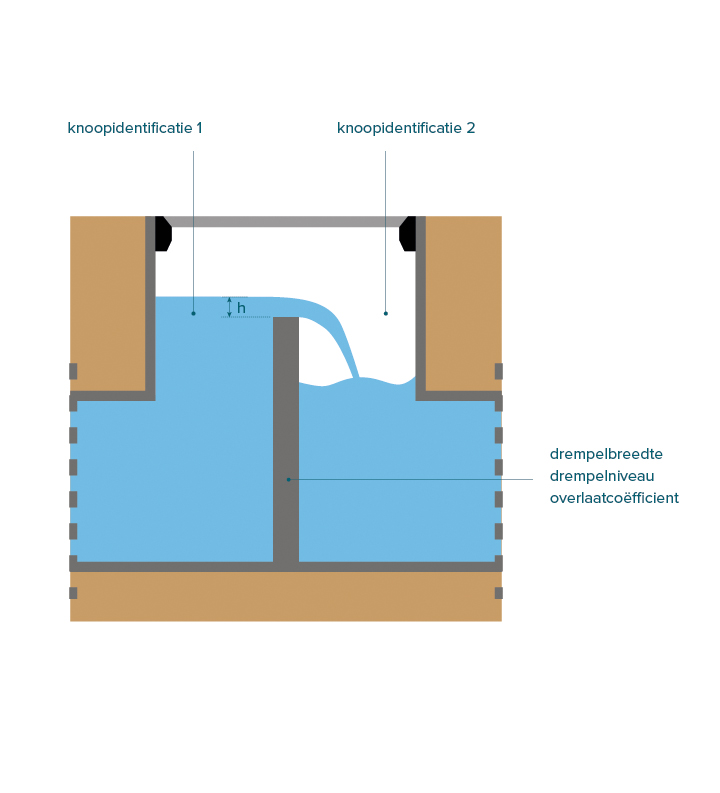
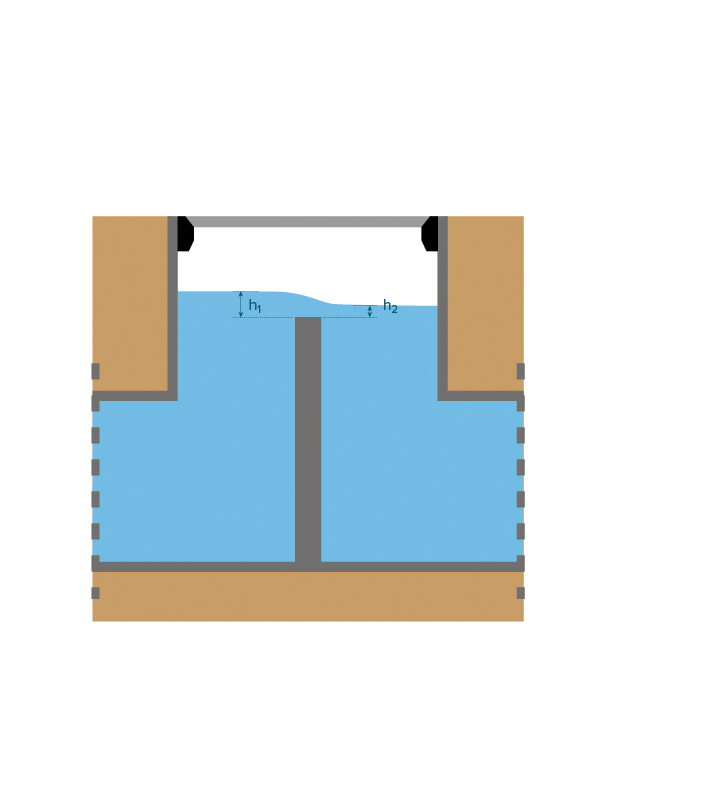
Default Q-h-relatie
Voor de relatie tussen waterstand en debiet over een overlaat gelden de volgende formules:
Volkomen:
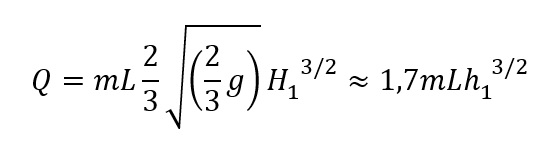
Zodra de benedenstroomse waterstand h2>2/3 h1 is, wordt gebruik gemaakt van de uitdrukking voor de onvolkomen overlaat:
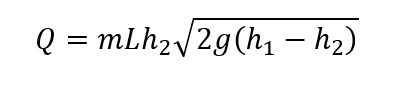
waarbij:
- Q : debiet (m3/s)
- L : lengte van de drempel (m)
- h1 : waterstand, bij lage aanstroomsnelheden gelijk verondersteld aan de energiehoogte H1, bovenstrooms van de drempel (m)
- h2 : waterstand benedenstrooms van de drempel (m)
- g : zwaartekrachtversnelling (9,81 m/s2)
- m : afvoercoëfficiënt (-)
De afvoercoëfficiënt m (ook vormfactor genoemd) is sterk afhankelijk van de aanstroming en de geometrie van de overlaatconstructie. Literatuurwaarden1 voor de vormfactor m zijn gebaseerd op laboratoriumresultaten onder bijna ideale omstandigheden. Gebruik als defaultwaarde voor de afvoercoëfficiënt m = 0,8. De m-waarden voor volkomen en onvolkomen overlaat zijn hierbij gelijk.
Drempellengte
In het verleden zijn regelmatig zeer lange drempels in betrekkelijk kleine putten gerealiseerd, de zogenaamde opgevouwen drempels (zie figuur A). Het is verleidelijk om de drempellengte in te voeren met de hiervoor genoemde parameterwaarden voor de Q-H-relatie. Maar dit is niet juist en kan tot een te hoog berekend debiet bij een gegeven waterstand leiden óf tot een te laag berekend waterpeil bij een gegeven debiet.
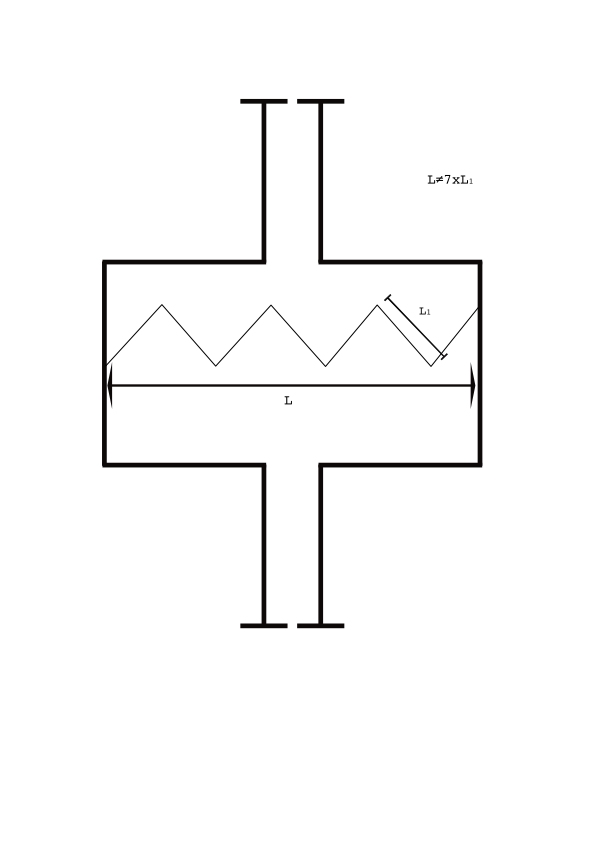
Brievenbus
In de praktijk komt het regelmatig voor dat de vrije hoogte tussen de overstortdrempel en de dekplaat van de put beperkt is. De dekplaat hindert dan de vrije afstroming over de overstort. U moet daarom de vrije hoogte meenemen in de schematisering.
De genoemde overlaatformules zijn niet meer toepasbaar als de (druk)hoogte bovenstrooms van de overstort de vrije hoogte overschrijdt. In plaats van een overlaatvergelijking moet u dan gebruik maken van een doorlaatvergelijking voor een rechthoekige doorlaat (“brievenbus”). Veel hydraulische software is in staat om automatisch te schakelen tussen de overlaatformule en de doorlaatformule. Let er bij het schematiseren op dat de afvoercoëfficiënten die u toegepast in de overlaatformule en de doorlaatformule op elkaar aansluiten.
Q-h-relatie in de praktijk
Uit praktijkmetingen2,3 is gebleken dat voor overstorten onder minder ideale praktijkomstandigheden van aanstroming en geometrie de volgende meer algemene relatie geldt (volkomen overlaat):
met 0,7 < α < 1,3 en 1,3 < β < 1,5.
Dit houdt in dat de debieten in de praktijk vaak lager zijn dan volgens de standaardformule berekend, of de bovenstroomse waterstand h1 hoger. Daarbij zijn grote verschillen mogelijk tussen individuele overstortconstructies.
Is er sprake van een kritische situatie waarbij de aanstromingscondities of de geometrie van de overstort niet ideaal zijn en waarbij een nauwkeurige Q-h-relatie cruciaal is (bijvoorbeeld bij een stuwput tussen twee bemalingsgebieden in een uitgestrekt gemengd rioolstelsel), dan wordt aanbevolen om de specifieke Q-h-relatie voor zowel volkomen als voor onvolkomen toestand te bepalen uit:
- Veldmetingen
- Laboratoriummetingen aan een (schaal)model
- Via numerieke CFD-berekeningen
Veldmetingen zijn het nauwkeurigst, gevolgd door metingen aan een model en in laatste instantie CFD berekeningen. Afhankelijk van de grootte en de complexiteit van de geometrie kunnen metingen kostbaar zijn. Een voorbeeld van de drie genoemde benaderingen en hun onderlinge samenhang is te vinden in Van Daal-Rombouts et al. (2017)4.
1 Idel'chik, I.E. (1966). Handbook of Hydraulic Resistance; Coefficents of Local Resistance and of Friction. Copyright Israel Program for Scientific Translations Ltd. IPST Cat. No. 1505.
2 RIONED (2001). Hydrodynamische modellen in de riolering; het proefschrift van prof. dr. ir. F.H.L.R. Clemens samengevat en bediscussieerd. ISBN 90·73·64-512·3. Stichting RIONED, Ede.
3 STOWA (2017). Evaluatie van sturing in stedelijke afvalwatersystemen; Samenvatting proefschrift Petra van Daal-Rombouts. STOWA-rapport 2017-32. ISBN/EAN 978.90.73645.60.8. Stichting RIONED, STOWA.
4 Van Daal-Rombouts, P., Tralli, A., Verhaart, F., Langeveld, J., & Clemens, F. (2017). Validation of computational fluid dynamics for deriving weir discharge relationships with scale model experiments and prototype measurements. Flow Measurement and Instrumentation, 58, 52-61.





