Het kalibratieproces

Hieronder staan de stappen beschreven.

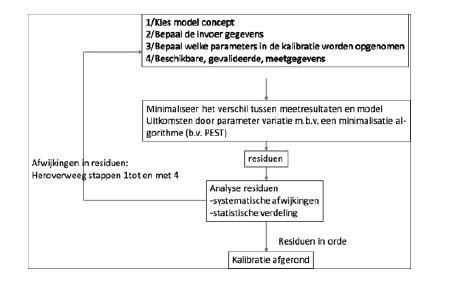
Parameterkeuze (stap 1)

Als eerste kiest u de kalibratieparameters. De keuze van het modelconcept definieert impliciet de benodigde invoerdata en de aard en het aantal van de (in principe) onbekende modelparameters. Bijvoorbeeld in een volledig rioleringsmodel is de hydraulische ruwheid een potentiële kalibratieparameter, maar in een vereenvoudigd rioleringsmodel niet.  

De keuze van de te kalibreren modelparameters is gecompliceerder dan u misschien in eerste instantie denkt. In principe zijn er bij een volledig hydrodynamisch model definitie Model in combinatie met een inloopmodel per leiding, per put en per individueel oppervlak vele onbekende parameters definitie Parameter. Zo kent elke leiding ten minste drie modelparameters: de hydraulische ruwheid, een instroomverliescoëfficiënt en een uitstroomverliescoëfficiënt. Daarnaast voeren op elke put meerdere typen oppervlakken af, waarvoor u per oppervlak de parameters van het inloopmodel moet bepalen. Zelfs voor een relatief klein stelsel van enkele honderden leidingen en putten leidt dit snel tot meer dan duizend onbekende parameters, nog afgezien van de overlaat- en doorvoercoëffiënten van bijzondere constructies. Deze 'zee' van onbekende parameters heet ook wel 'the curse of dimensionality' (vrij vertaald: 'het is makkelijk te verdwalen in een n-dimensionale ruimte').

In de praktijk is het niet haalbaar om heel veel parameters te kalibreren, omdat u dan een enorme hoeveelheid meetgegevens nodig hebt. U kunt dit probleem omzeilen door parameters samen te voegen ('lumpen'), een benadering die zich in de praktijk heeft bewezen. Hierbij gaat u ervan uit dat de ruwheidswaarde van alle leidingen en de lokale verliesparameters gelijk zijn. Ook veronderstelt u dan dat de inloopparameters per type oppervlak niet variëren tussen individuele oppervlakken van hetzelfde type. Zo kunt u het aantal onbekende parameters flink reduceren (in de praktijk tot een maximum van circa 10) en kunt u toch bruikbare resultaten behalen.

N.B. Invoergegevens zoals oppervlak van putten, pompcapaciteiten en geometrie van elementen mag u in het model niet als te kalibreren parameter meenemen. Deze categorie data behoort immers tot de ‘vaste’ invoergegevens van een model die voortkomen uit de inventarisatie vóór de opbouw van het rekenmodel.

Parameteroptimalisatie (stap 2)

In de tweede stap zoekt u de beste combinatie van parameters waarmee het gebruikte model de meetresultaten zo goed mogelijk reproduceert. (N.B. De gevonden parameterset reflecteert geen fysische werkelijkheid, maar eerder de beste parameterwaarden gegeven het model, de invoer van structuur en geometrie en de hoeveelheid en kwaliteit van de beschikbare meetdata.) Bij een eerste poging zijn er meestal belangrijke systematische verschillen tussen modelresultaat en gemeten resultaat (residuen).

Het doel van parameteroptimalisatie is om het verschil tussen gemeten en berekende waarden te minimaliseren (in de regel gaat het om waterstanden en/of debieten definitie Debiet als functie van de tijd). Hiervoor is een scala aan wiskundige technieken voorhanden. De eenvoudigste en bekendste (en dus in de praktijk vaak toegepaste) methode is die van de kleinste kwadraten, een bijzonder geval van een techniek die bekend is als Maximum Likelihood Estimates (MLE). Hierbij zoekt u naar een parameterset die de volgende grootheid S minimaliseert: 

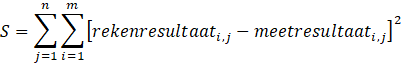
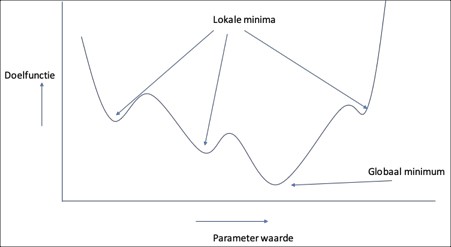
waarbij rekenresultaat_i,j betrekking heeft op een berekend resultaat (waterstand of debiet) op een meetlocatie j op tijdstip i en meetresultaat_i,j betrekking heeft op het corresponderende gemeten resultaat. De grootheid S wordt geminimaliseerd afhankelijk van het rekenmodel en de beschikbare meetdata. Als u de kalibratie correct hebt uitgevoerd, vindt u het best passende resultaat dat mogelijk is onder de gegeven omstandigheden (zie figuur B). Als er dan afwijkingen overblijven, moet u deze zoeken in:

• fouten in de invoergegevens;
• fouten in de meetdata;
• geldigheid van het gebruikte model (als bijvoorbeeld de gemeten neerslag is gevallen in de vorm van sneeuw, zijn de meestal gebruikte inloopmodelconcepten niet meer van toepassing). 

Uitvoering

Voor elke combinatie van modelparameters krijgt u een iets ander resultaat, daarom is S op te vatten als een functie van de modelparameters. Figuur B geeft een fictief voorbeeld van een S die slechts van één parameter afhankelijk is. Zoals u ziet, kan een dergelijke functie meerdere minima hebben. Iets dergelijks kan ook gelden voor een situatie met meerdere parameters, wat vaak duidt op een probleem met het model, de parameterkeuze of de kwaliteit van de metingen. In praktische toepassingen zet u dan ook vaak eerst een algoritme (meestal een genetisch algoritme) in om een globale verkenning te doen van S, zodat u globaal weet of, en zo ja waar, zich lokale minima bevinden. Daarna bepaalt u met andere algoritmen (bijvoorbeeld een multidimensionaal Newton-Rhapson- of Levenberg-Marquart algoritme) de ligging van de lokale minima nauwkeuriger. Als alternatief kunt u ook de eerste stap overslaan en met een aantal onderling verschillende beginschattingen van de modelparameters direct naar het globale minimum zoeken. Als u voor meerdere beginschattingen van de modelparameters identieke eindresultaten krijgt, dan kunt u dit resultaat als eindresultaat aannemen.

Software en handleiding

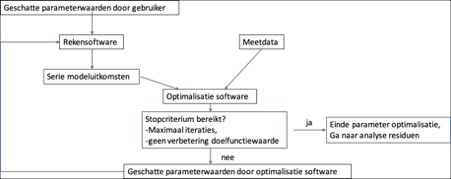
Het uitvoeren van de parameteroptimalisatie is nogal specialistisch werk, waarvoor soms maatsoftware wordt geschreven. Er wordt ook vaak gratis beschikbare software gebruikt, zoals PEST (Parameter ESTimator), deze kunt u downloaden via Pesthomepage. Op deze website staan ook een goede handleiding en wat achtergronden van de parameteroptimalisatie. Figuur C geeft schematisch weer hoe u een rekenmodel met een optimalisatiealgoritme in een ‘master-slave-relatie' plaatst (zie figuur C). Het is een iteratief proces waarbij u voor de meeste algoritmen per iteratie n+1 (waarbij n het aantal onbekende parameters is) volledige modelberekeningen uitvoert. Dit illustreert nogmaals de noodzaak om het aantal te kalibreren parameters niet te groot te kiezen, dat leidt immers al snel tot een praktisch onuitvoerbare rekenpartij. 

Resultaat

Het resultaat van de parameteroptimalisatie is een set modelparameters die leidt tot de best mogelijke overeenkomst tussen het gebruikte model en de beschikbare meetdata. Is de overeenkomst naar uw mening niet goed genoeg, dan staan de volgende opties open:

• U kunt de juistheid van de modelkeuze en de bijbehorende kwaliteit van de gebruikte gegevens nader bestuderen.
• U kunt de gebruikte meetdata en mogelijk de meetopzet kritisch evalueren (ofwel: heb ik genoeg en voldoende juiste meetdata om de kalibratie uit te voeren?).
• U kunt een relatie leggen met de onderhoudstoestand van het systeem. Marco van Bijnen heeft overtuigend aangetoond dat de onderhoudstoestand van een systeem zich vertaalt in meetbare veranderingen in het gedrag van een systeem, die via modelkalibratie definitie Modelkalibratie zijn te kwantificeren.¹
• U kunt erin berusten en de modeluitkomsten met de nodige voorzichtigheid gebruiken.

Analyse van de residuen (stap 3)

Zodra u de parameteroptimalisatie met succes hebt doorlopen, moet u beoordelen of het verkregen resultaat voldoet. In deze laatste stap gaat u na of, en zo ja in hoeverre, de gevonden parameterset (eventueel na aanpassing van het modelconcept en/of de invoergegevens) overdraagbaar is naar andere, niet in de kalibratie meegenomen, gemeten gebeurtenissen. Aan de hand van de residuen kunt u hiervoor enkele objectief toetsbare eisen formuleren. 

In de praktijk zal ook na parameteroptimalisatie de waarde van de doelfunctie S nooit exact nul zijn. Dit betekent dus dat er (kleine) verschillen tussen metingen en modeluitkomsten blijven bestaan. Dat kan komen door meetonnauwkeurigheid (niet te vermijden), een model dat niet alle relevante processen meeneemt of fouten in de invoer (structuur en geometrie, afvoerend oppervlak en neerslag). Daarnaast geeft de structuur van de residuen in tijd en plaats vaak belangrijke aanwijzingen in welke richting u de oorzaak moet zoeken.In stap 3 analyseert u deze verschillen en krijgt u aanwijzingen waar het probleem zit (in het modelconcept, de parameterkeuze, de invoergegevens of de meetresultaten). Zodra er geen systematische verschillen tussen model en metingen meer zijn óf geen verbetering meer mogelijk is gegeven de beschikbare middelen (instrumenten, tijd en budget), rondt u de kalibratie af.

Een van de onderliggende aannamen in het parameteroptimalisatieproces is dat de residuen geen onderlinge samenhang vertonen in tijd en plaats. Dit houdt bijvoorbeeld in dat als op een meetlocatie gedurende een langere periode (zo'n 15 minuten) de residuen allemaal positief of allemaal negatief zijn, sprake is van een systematische afwijking.

Verder lezen

Meer details en achtergronden vindt u in "Hydrodynamic models in urban drainage application and calibration" (Clemens, 2001).

¹ Van Bijnen, J.A.C. (2018). The impact of sewer condition on the performance of sewer systems. (Proefschrift) Technische Universiteit Delft, Delft.